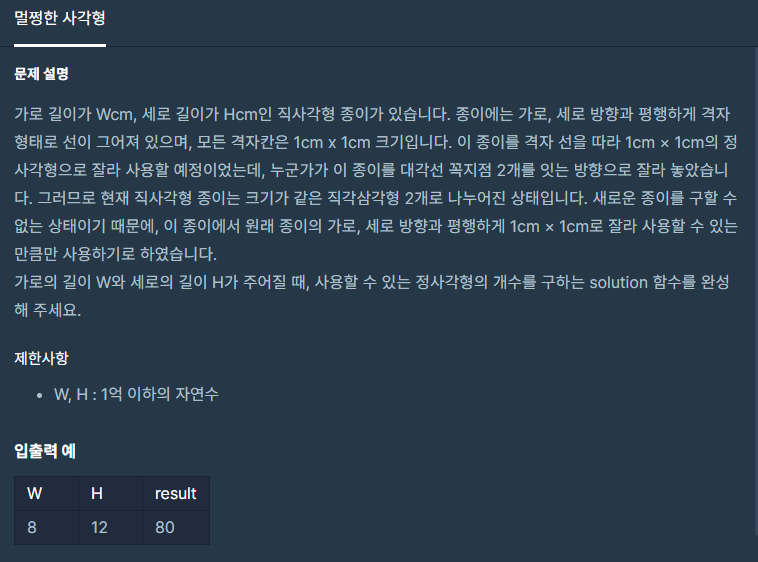

멀쩡한 사각형 찾기 문제 최대공약수 풀이법이 핵심입니다.
예시-> 8과 12로 80을 뽑는 식을 풀어봅시다. (최대 공배수 영어로 gcp입니다)
8과 12의 gcp 구하면 4입니다. 도형이 4개가 나옵니다. 이 의미가 뭐냐면
각각 공배수로 나누면 2, 3이나 오는데 2칸과 3칸을 쓴 도형이 4번 나온다는 의미입니다.
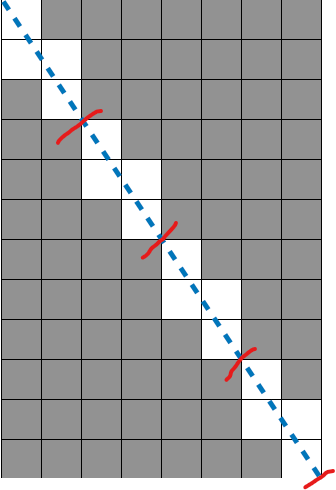
만약 6과 2를 했다면 gcp는 2이고 같은 패턴 2개를 사용한 도형이 나옵니다.
여기서도 동일하게 가로, 세로 값을 gcp로 나눠주면 3, 1 짜리 도형이 나오는데 gcp개수만큼 나옵니다.

여기까지 패턴의 개념은 이해하셨으리라 봅니다 근데 문제풀이를 위해서는 못쓰는 사각형 개수를 구해야 합니다.
그럼 1, 3 짜리 도형을 예로 들었을 때 대각선이 그어진다면?
가로 1칸에 세로 3칸짜리 직사각형에 대각선을 그으면 다 그어집니다.
이때는 네모칸 개념으로 봐야 하는데 세로 네모는 가로 1, 세로 1이 3개인 거고 가로 네모는 가로 1, 세로 1이 1개입니다.
즉 세로네모는 이미 가로를 가지고 있기 때문에 기본가로가있습니다.
세로 3칸 그어지는 거 + 가로 칸수 개념인데
세로 칸(3칸) + 가로 칸(1칸) - 세로의 기본 칸(1칸) 대각선 그어진 사각형의 개수는 이런 식으로 구할 수 있습니다.

이해를 돕기 위해 다시 기본 예제로 돌아와 봅니다.
예제의 gcp는 4입니다. 2, 3짜리 직각 사각형 즉 가로 2, 세로 3의 사각형이 4개 생기는 구조입니다.
위에 설명했던 1, 3짜리의 경우 세로 3칸이 다 그어집니다. 하지만 여기는 가로 2칸이 있습니다.
즉 그어지면서 칸을 한 칸 옮긴다는 건데 그래서 넘어가는 구간만큼 +1을 해줘야 합니다.
그럼 뭐다? -> 세로 칸(3칸) + 가로 칸(2칸) - 세로 기본 칸(1칸) 개념입니다.
원래 세로 3 가로 1일 경우 원래 3칸 그을건대 가로가 +1이 됐으니까 가로 칸이 옮겨지면서 2칸이 그어지는 구간이 무조건 생깁니다.
이제 문제풀이 할 건데 위에 패턴 이해가 안 되셨다면 제 설명이 부족했을 수도 있으니 꼭 어디서든
그 패턴을 이해하고 밑에 답을 봐주시면 좋을듯합니다.
식자체는 간단합니다. w 던 h 던 대입해서 최대 공배수를 구할 겁니다.
for문에 둘 중 하나의 최대치부터 -- 식을 진행하는 문장을 만들어줍니다.
그리고 값을 내리면서 둘 다 %로 나누었을 때 나머지 0인 경우가 최대 공배수입니다.
(만약 더 작은 값을 for문에 넣어서 효율을 늘리고 싶다면 여러분은 if문 넣으시면 됩니다)
문제를 따라가 봅시다. -> 총 칸수 - 그어진 칸 값 값을 리턴하는 건데 그어진 칸 공식은 위에 패턴 설명한 그대로입니다.
(가로/최대공약수 + 세로/최대공약수 -1 ) = 가로 칸 + 세로 칸 - 기본 칸 이 개념입니다.
여기서 패턴 나온 개수 곱해줘야 되니까 최대 공배수 곱해주는 겁니다.
function solution(w, h) {
for(let i =w; 0<i; i--){
if(w%i==0 && h%i==0)return (w*h)-((w/i+h/i-1)*i)
}
}
i가 최대 공배수일 때 if문 통과하고 정답 리턴하는 식입니다. 성실한 코딩 하세요.
